Foundations of the Modern World – Mathematical Basis
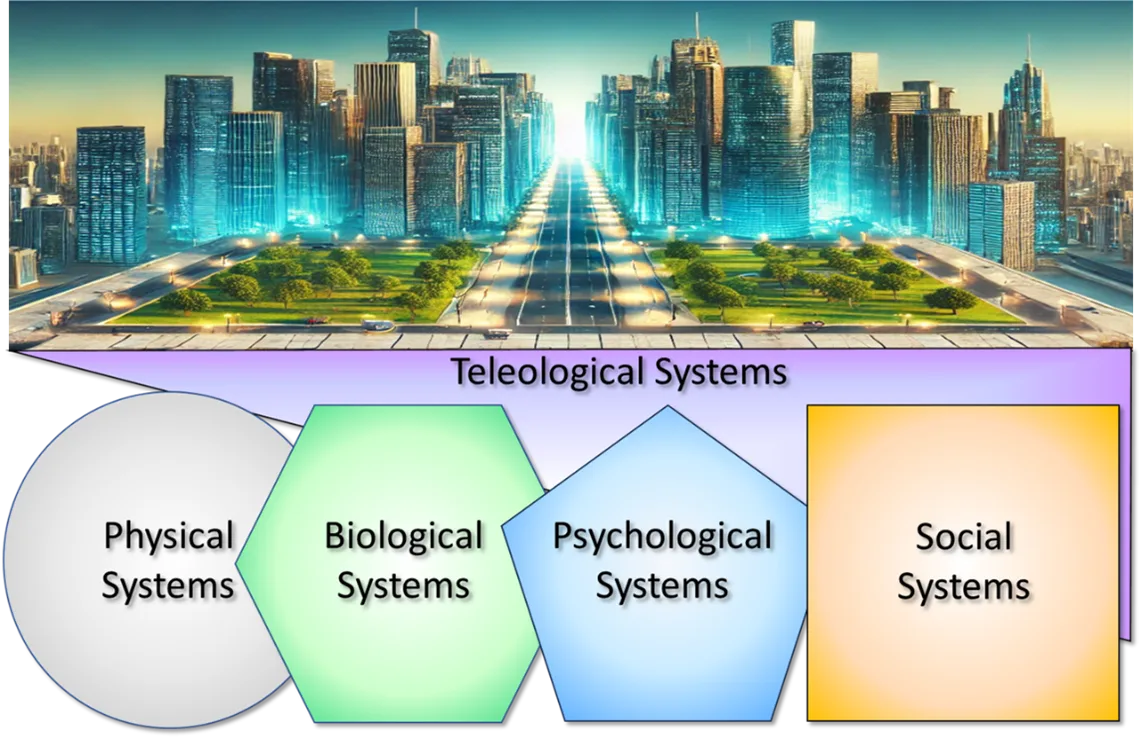
Consider the structure of the following diagram as a conceptual model for the key functions of the modern world.
The diagram shows the layered interaction of five foundational systems, each building on the capabilities of the previous. At the heart of this framework is the recognition that mathematics is essential to analyzing, modeling, and guiding the behavior and interaction of these systems. Here's an explanation of each system and their interrelations:
1. Physical Systems
- Shape: Circle
- Color: Stone Gray
- Contents: Inert matter, energy, and information
- Examples: Particles, atoms, molecules, air, fluids, rocks, rivers, mountains, continents, planets, stars, galaxies
- Key Traits: Do not have life or intent but exhibit complex behavior from simple laws like gravity, thermodynamics, and electromagnetism
- Mathematical Role:
The instantaneous behavior of small systems can be modeled using simple equations. Larger systems require more complex mathematics to understand behaviors over time.Mathematics is the language of physical reality, enabling us to build everything from bridges to computer chips.
2. Biological Systems
- Shape: Hexagon
- Color: Leaf Green
- Contents: All elements of Physical Systems, plus life processes
- Examples: Bacteria, fungi, insects, fish, birds, mammals, humans
- Key Traits: Add reproduction, metabolism, sensing, choosing, and acting. These systems adapt, evolve, and self-regulate
- Mathematical Role:
Modeled using systems biology, nonlinear dynamics, and information theory.Biology is computation in motion, with mathematics describing everything from gene expression to neural networks.
3. Psychological Systems
- Shape: Pentagon
- Color: Sky Blue
- Contents: All elements of Biological Systems, plus conscious cognition
- Examples: Primates, dolphins, whales, octopuses, crows, parrots, horses, dogs, cats
- Key Traits: Consciousness, emotions, memory, hierarchies of needs and desires (e.g., Maslow’s hierarchy). These systems form goals and make complex decisions
- Mathematical Role:
Studied through decision theory, probability, and dynamic systems.Mathematics helps model the mind—simulating decision-making, attention, and learning.
4. Social Systems
- Shape: Square
- Color: Harvest Orange
- Contents: All elements of Psychological Systems, plus interactions between individuals
- Examples: Ant hills, bee hives, ecosystems, families, communities, cities, nations, businesses, governments
- Key Traits: Enable language, collective learning, culture, technology, economics, and group dynamics
- Mathematical Role:
Analyzed through network theory, game theory, statistics, and complex systems modeling.Mathematics enables us to optimize and govern society—from traffic flows to stock markets and social networks.
5. Teleological Systems
- Position: Above all
- Color: Royal Purple
- Definition: From the Greek telos (end, purpose). These systems define the goals, values, and success criteria that guide the other four systems
- Examples: Founding stories, hero stories, values, morals, ethics, legal systems, religions, mission statements
- Key Traits: Embody intentionality, ethics, and long-term vision; shape policies, institutions, and strategy
- Mathematical Role:
Expressed in optimization theory, control systems, and value alignment frameworks.Mathematics helps us define and reach our goals—not just describe the world as it is, but guide it toward what it could be.
Note: The Foundations Model does not prescribe a set of beliefs. Instead, it shows how values affect actions, and how outcomes inform whether our beliefs or systems should evolve.
Final Insight: The Modern World as a System of Systems
The modern world—represented metaphorically by an advanced city—is the result of interactions across these five systems. Each layer builds upon the previous:
- Skyscrapers depend on physical laws
- Healthcare depends on biological understanding
- Education and mental health rely on psychological principles
- Markets and democracies operate through social systems
- Ethics and sustainability stem from teleological thinking
Mathematics is the connective tissue, enabling us to model, simulate, and optimize each layer of modern life.
How This Relates to TeachRealMath
All content developed by ActiveLearningLabs connects to this model. Our math activities:
- Help students see the big picture
- Relate abstract math to personal, societal, and global contexts
- Include both quantitative and qualitative modeling
- Promote first-order decision-making using approximation and logic
We recognize that no model is perfect—but even imperfect models offer critical guidance for understanding and improving the world.
Join the Discussion
We invite you to explore and share how models—mathematical and conceptual—can enable better outcomes for students, teachers, and communities.